Escales
“Scales són funcions que assignen a partir d'un domini d'entrada un rang de sortida.”
Aquesta és la definició de les scales de D3 de Mike Bostock’s .
Els valors en qualsevol conjunt de dades és poc probable que es corresponguin exactament amb les dimension en píxles del svg a on s'han de visualitzar. Scales proporcionen una manera fàcil d'adaptar els valors inicials als valors que encaixin amb les dimensions de l'espai de visualització.
Les Scales de D3 són funcions, els paràmetres de les quals s'han de definir.
Un cop creades, quan es crida a la funció d'escala ,s'hi envien les dades inicial (el domini d'entrada), aquesta els transforma en un conjunt de dades adaptat al marc de visualització.
Podeu definir i usar tantes escales com vulguis .
Pots estar temptat de pensar en una escala com un conjunt de marques de graduació que indica una progressió de valors que apareix a la visualització. No et deixis enganyar!
Aquestes marques de graduació són part d'un eix , que és essencialment una representació visual d'una escala.
Per a D3 una escala és una relació matemàtica, sense sortida visual directa. Has de pensar en escales i eixos com dos termes diferents, però amb elements relacionats.
Aquest capítol només parla d'escales lineals, que són les més comuns i les més entendores. Un cop hagis entés bé les escales lineals, les altres no et costaran gaire esforç.
Pomes i Píxels
Imagineu que el següent conjunt de dades representa el nombre de pomes venut en una fruiteria cada mes:
var dataset = [ 100, 200, 300, 400, 500 ];
Primer de tot, és una gran notícia. La botiga ven 100 pomes més cada mes! El negoci va de nassos!.
Per mostrar aquest èxit, vol fer un gràfic de barres que il·lustri l'ascens empinat de les vendes de la poma, en el que cada valor de venda mensual es corresopongui a l'altura d'una barra del diagrama.
Fins ara , hem utilitzat els valors de dades directament com a valors de visualització , fent cas omís de les diferències entre unitats. Així, si es van vendre 500 pomes, la barra corresponent seria de 500 píxels d'alçada.
Això podria anar bé, però què passa amb el mes que ve, quan es venen 600 pomes?. I un any més tard, quan es venen 1,800 pomes?. Els que volguessin veure-ho haurien de comprar pantalles cada cop més grans, només per ser capaços de veure tota l'alçada d'aquestes barres!
Aquí és on entra el mètode scales(). Com que les pomes no són píxels ( i tampoc són taronges ) , necessitem escales per fer-ne la traducció.
Dominis i Rangs
El domini d'entrada del mètode scales és el ventall de possibles valors de dades d'entrada. En el conjunt de dades anteriors (venda de pomes mensuals), el domini d'entrada tindria un valor mínim de 100 i un de màsim de 500 o també el podriem establir entre (zero) 0 i 500 .
El rang de sortida del mètode scales és el ventall de possibles valors de sortida per a ocupar tot, o la part que es vulgui de l'element del DOM, a on han de veure's les dade, la unitat que normalment es fa servir és el píxel.
El rang de sortida és totalment decisió teva, o del dissenyador de la informació. Si vostè decideix que la barra de vendes mensuals de pomes més curta sigui de 10 píxels d'alçada i la més alta sigui de 350 píxels d'alçada , llavors et cal establir un rang de sortida entre 10 i 350 .
Per exemple, creeu una escala amb un domini d'entrada de 100,500 i un rang de sortida de 10,350 .
Com que has definit el valor inferior del domini d'entrada en 100 , et retornarà el valor inferior del rang de sortida que és 10.
Com que li has donat un valor de 500 al valor máxim del domini d'entrada, et retornarà el valor màxim del rang de sortida, que en aquest cas l'has definit amb un valor de 350 .
Els valors intermitjos es calculen proporcionalment, és a dir a un valor d'entrada per aquesta escala de 300 que és al mig del domini, retornaria un valor de 180 que és al mig del rang de sortida.
Podríem visualitzar el domini i el rang com a eixos amb diferents "escales" que van de costat a costat.
Una cosa més: Tenint en compte que és molt fàcil barrejar el domini d'entrada i el rang de sortida ,m'agradaria proposar-te un exercidi de terminologia, per aclarir-nos. Quan digui "d'entrada " , tu dius "domini" . Quan diguid "sortida", tu diues "rang". A punt? Som-hi!
- Input! Domain!
- Output! Range!
- Input! Domain!
- Output! Range!
Ho tens? Fantàstic.
Normalització
Si està familiaritzat amb el concepte de normalització , et pot ser útil saber que, amb una escala lineal, això és el que s'està produint.
La normalització és el procés d'assignar a un valor numèric un nou valor entre 0 i 1, en funció d'uns valors mínims i màxims predefinit.
Per exemple amb 365 dies a l'any, el dia número 310 li pertorca aproximadament el valor 0,85 , o el que és el mateix està al 85% de la llargada de l'any.
Amb escales lineals , només estem deixant que D3 gestioni les opracions matemàtiques del procés de normalització. El valor d'entrada es normalitza d'acord amb el domini (recorda: vol dir valors d'entrada) i, a continuació, el valor normalitzat es escalat pel rang (valors de sortida).
Creant una escala
S'accedeix al Generador d'escales de D3 amb d3.scale, seguit pel tipus d'escala que es desitja.
var escala = d3.scale.linear();
Enhorabona! Ara escala és una funció a la qual es pot passar valors d'entrada. ( No es deixi enganyar pel var anterior; recordi que a JavaScript , les variables poden emmagatzemar funcions. )
escala(2.5); //Retorna 2.5
Ja que no hem establert cap domini ni cap rang, aquesta funció fa servir l'escala 1: 1 . És a dir , tot el entra es retorna sense canvis.
Podem establir com a domini d'entrada per l'escala els valors 100,500 al passar aquests valors al domini() com una matriu :
escala.domain([100, 500]);
Ajusta el rang de sortida de manera semblant, amb range():
escala.range([10, 350]);
Aquests passos es poden realitzar per separat, com l'anterior, o encadenats junts en una sola línia de codi
var escala = d3.scale.linear()
.domain([100, 500])
.range([10, 350]);
I d'aqueta manera, ja tenim l'escala preparada!
escala(100); //Retorna 10
escala(300); //Retorna 180
escala(500); //Retorna 350
En general , es fa la crida a la funció "escala" dins d'un mètode attr ( ) o similar, i no directament.
Ara modificarem el nostre gràfic de dispersió fent servir escales dinàmiques.
Escalant el nostre gràfic de dispersió
Revisem el nostre conjunt de dades del gràfic de dispersió:
var dataset = [
[5, 20],
[480, 90],
[250, 50],
[100, 33],
[330, 95],
[410, 12],
[475, 44],
[25, 67],
[85, 21],
[220, 88]
];
Recordaràs que el conjunt de dades és una matriu de matrius. Hem traçat el primer valor de cada matriu sobre l'eix x , i el segon valor sobre l'eix y.
Comencem amb l'eix x.
Només fent una ullada als valors de x, sembla que van des de 5 fins a 480, de manera que un domini raonable d'entrada podria ser de 0,500 , oi ?
… Per què em mires d'aquesta manera?
Ahh, perquè vols mantenir el teu codi flexible i escalable , de manera que funcioni fins i tot si es canvien de dades en el futur. Molt intel·ligent!.
En lloc d'especificar valors fixos pel domini, podem fer servir algunes funcions de matriu convenients com ara min () i max () per analitzar sobre la marxa, quins són els valors mínim i màxim de les nostres dades.
Per exemple, aquest codi fa un bucle a través dels valors de x del nostre conjunt de dades i retorna el valor més gran:
d3.max(dataset, function(d) { //Retorna 480
return d[0]; //Fa referència al primer valor de la nostra sub-matriu
});
Posem-ho tot junt, per crear l'escala pel nostre eix x:
var EscalaX = d3.scale.linear()
.domain([0, d3.max(dataset, function(d) {
return d[0];
})])
.range([0, w]);
En primer lloc, fixa't que li he posat de nom EscalaX . Per descomptat, pots nomenar les teves escales com vulguis, però un nom com
EscalaX ajuda a recordar que fa aquesta funció.
En segon lloc, fixa't que he posat l'extrem inferior del domini d'entrada a zero. (També podeu fer servir min () per calcular un valor dinàmic.) L'extrem superior del domini s'estableix en el valor màxim del conjunt de dades (que és de 480).
Finalment, fixa't que el rang de sortida s'estableix en 0 i w , l'amplada de la SVG.
Farem servir un codi molt similar per crear la funció d'escala per a l'eix y:
var EscalaY = d3.scale.linear()
.domain([0, d3.max(dataset, function(d) {
return d[1];
})])
.range([0, h]);
Recordeu que el mètode max () s'aplica sobre les dades d[1] , que son els valors segons de cada sub-matriu. A més, l'extrem superior del rang () s'estableix en h en lloc de w .
Les funcions d'escala estan al seu lloc! Ara tot el que necessitem és fer-les servir. Només has de modificar el codi on varem crear les coordenades per a cada circle
.attr("cx", function(d) {
return d[0];
})
així retorna el valor "escalat" (en lloc del valor original):
.attr("cx", function(d) {
return xScale(d[0]);
})
De la mateixa manera, per a l'eix y, aquest
.attr("cy", function(d) {
return d[1];
})
es modifica com:
.attr("cy", function(d) {
return yScale(d[1]);
})
Per si fos poc, farem el mateix canvi en què establim les coordenades per a les etiquetes de text, de manera que aquestes línies/p>
.attr("x", function(d) {
return d[0];
})
.attr("y", function(d) {
return d[1];
})
siguin aquestes:
.attr("x", function(d) {
return xScale(d[0]);
})
.attr("y", function(d) {
return yScale(d[1]);
})
I aquí està!

Visualment, és decebedorament similar al nostre diagrama de dispersió original! No obstant això, estem fent més progressos del que poden ser evidents.
Perfeccionant la sortida a pantalla
Pots haver-te fixat que els valors de y més petits estan al capdemunt del gràfic, mentre que els més grans estan cap a la part inferior. Ara que estem fent servir escales, és molt fàcil canviar això, de tal manera que els valors més grans estiguin cap a la part superiror, com era d'esperar. És només una qüestió de canviar el rang de sortida de EscalaY
.range([0, h]);
per
.range([h, 0]);

Aquí tens el codi. Sí, ara un valor d'entrada menor a l'EscalaY produirà un valor de sortida major , que empeny els cercles i els elements de textcap a baix, o sigui més a prop de la base de la imatge. Ho sé, és gairebé massa fàcil!
Encara alguns elements queden tallats. Introduim doncs una variable pel padding:
var padding = 20;
Llavors incorporarem el valor del padding quan fixem el rang de les dues escales. El rang de EscalaX era rang ([0, w]) , i ara serà
.range([padding, w - padding]);
El rang per l'EscalaY era range([h, 0]), peró ara serà
.range([h - padding, padding]);
Això ens dona 20 píxels de marge a tot voltant del marge de l'SVG:

No obstant això, les etiquetes de text de l'extrem dret encara queden tallades, així que duplicarem la quantitat de l'EscaleX perque en quede el doble de marge a la part dreta:
.range([padding, w - padding * 2]);

Millor! Aquí tnes el codi fins al moment.
Però hi ha un canvi més que m'agradaria fer. En lloc d'establir el radi de cada circle com l'arrel quadrada del seu valor de i (que és un valor complex, i tampoc aporta res), per què no fem una altra escala personalitzada?
var EscalaR = d3.scale.linear()
.domain([0, d3.max(dataset, function(d) {
return d[1];
})])
.range([2, 5]);
Després de fixar el radi es veu així:
.attr("r", function(d) {
return rScale(d[1]);
});
Això és emocionant, perquè estem garantint que els nostres valors del radi cauen sempre dins del rang establert entre 2,5. (O gairebé sempre :. Veure la referència que hi ha a continuació a clamp () ) Així pels valors de dades de 0 (l'entrada mínima) aconseguirà cercles de radi 2 (o un diàmetre de 4 píxels). Amb el valor de radi més gran obtindrà un cercle de radi 5 (diàmetre de 10 píxels).

Voila: La nostra primera escala utilitzat per a una propietat visual que no sigui un valor de l'eix.
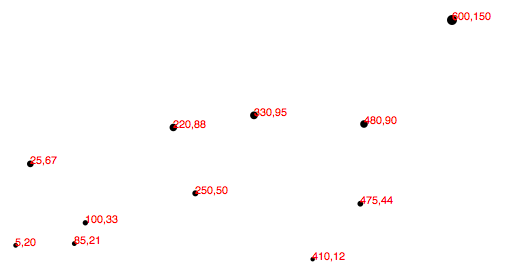
Finalment, per si de cas el poder d'escales encara no t'ha seduit, m'agradaria afegir una varietat nés al conjunt de dades: [600, 150]

Boom! Aquí hi ha el codi. Observa com tots els punts anteriors mantenen les seves posicions relatives, però han migrat i estan més a prop entre ells, més cap a baix i més cap a l'esquerra, per donar cabuda al nouvingut.
I ara, una revelació final: Ara es fàcil canviar la mida del nostre SVG. Automàticament es canvien totes les escales. Aquí, he augmentat el valor de h de 100 a 300 i no he canviat res més.:
Boom, un altre cop! Aquí tens el codi actualitzat. Espero, que estiguis veient això i adonant-te que: No més nits en blanc austant el codi perquè el client ha decidit que el gràfic ha de ser de 800 píxels d'ample en lloc de 600. Sí, tindràs més hores de son gràcies a mi (i als brillants mètodes incorporats a D3) . Estar ben descansat és un avantatge competitiu. Podràs agrair-m'ho més endavant.
Altres mètodes
d3.scale.linear() té diversos altres mètodes útils que mereixen ser comentats:
nice()— Això li diu a scale() que arrodoneixi els valors del domini d'entrada al valor més sencer més proper. Des del wiki de D3: "Per exemple, per a un domini de [,20147987687960267,, 996679553296417], el domini és més agradable si és [0.2, 1]." Això és útil per a la gent normal, que tenen dificultats per llegir nombres com, 20147987687960267.rangeRound()—Fes servirrangeRound()en lloc derange()i tots els valors de sortida s'arrodonirant al valor serncer més propoer. Això és útil si vols formes abm un número exacte de píxels, que eviti contorns difuminats que poden tenir problemes de visualització tot i l'antialiasing.clamp()— Per defecte, una escala lineal pot retornar valors fora del rang especificat. Per exemple, si se li dóna un valor fora del domini d'entrada esperat, una escala retornarà un nombre també fora del rang de sortida. Crida a.clamp (true)en una escala,i obliga a tots els valors de sortida a estar dins del rang especificat. Això vol dir que els valors excessius seran arrodonits al valor inferior o superior de la gamma (el que sigui més proper).
Altres Scales
A part de linear scales (de les que hem parlat fins ara), D3 té altres tipus de métodes incorporats:
identity— Una escala 1: 1, útil sobretot per a valors de píxelssqrt— Una escala amb proporció d'arrel quadradapow— A power scale (good for the gym)log— A escala logarítmicaquantize— Una escala lineal amb valors discrets per entrades fora del domini, per quan vols ordenar dades en paquetsquantile— Semblant a l'anterior, però amb valors discrets pel seu domini d'entrada (quan ja tens paquets)ordinal— Escales ordinals que utilitzen valors no quantitatius (com noms de categories) per a la sortida; perfecte per comparar pomes i taronges
Ves al següent capítol: Eixos →